10 поразительных парадоксов, которые сбивают с толку

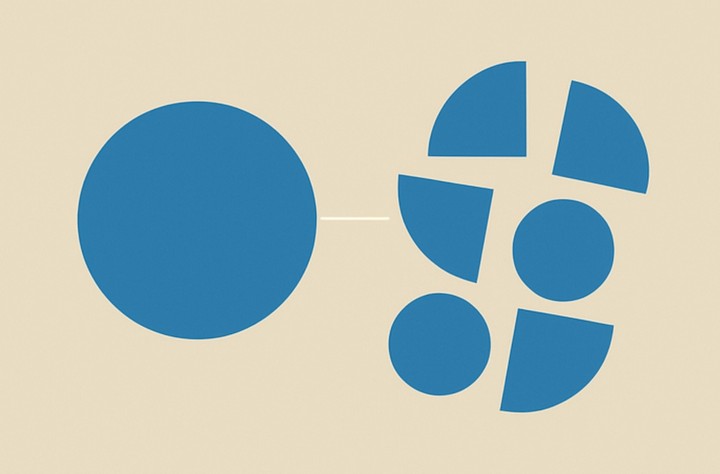
Представьте, что вы держите в руках шар. А теперь вообразите, что вы разрываете этот шар на части — на любые фрагменты произвольной формы. Затем вы собираете эти части обратно, но уже не в один, а в два шара.

Согласно теоретико-множественной геометрии, вещество исходного шара можно разделить и пересобрать таким образом, чтобы получить два шара, точно такого же размера и формы, как оригинал. Более того, если у вас есть два шара разного объёма, любой из них можно преобразовать в другой.

Из этого следует парадоксальный вывод: горошину можно разделить и трансформировать в шар размером с Солнце.

Главный трюк парадокса

Ключевой момент парадокса в том, что допускается разделение шара на части абсолютно любой формы. В реальности это невозможно: вы ограничены структурой материи и, в конечном счёте, размерами атомов.

Чтобы действительно произвольно разделить шар, он должен содержать бесконечное число доступных нуль-мерных точек. Такой шар был бы бесконечно плотным. После разделения эти сложные формы могли бы не иметь определённого объёма. Их можно было бы перестроить в шар любого размера. Каждый новый шар также содержал бы бесконечное число точек и был бы бесконечно плотным.

Хотя на практике это невозможно реализовать с физическими объектами, парадокс работает в математике, где речь идёт о сферах — бесконечно делимых множествах чисел в трёхмерном пространстве.

Разрешение парадокса, называемое теоремой Банаха — Тарского, имеет важное значение для теории множеств в математике.