Закон Бенфорда

Почему так часто встречается цифра 1?

Какова вероятность того, что случайное число начнётся с цифры «1»? Или с «3» или «7»? На первый взгляд, зная основы теории вероятностей, можно предположить, что каждая из девяти возможных начальных цифр (от 1 до 9) встречается примерно одинаково часто — около 11,1%. Однако на практике это далеко не так.

Реальные данные и неожиданная закономерность

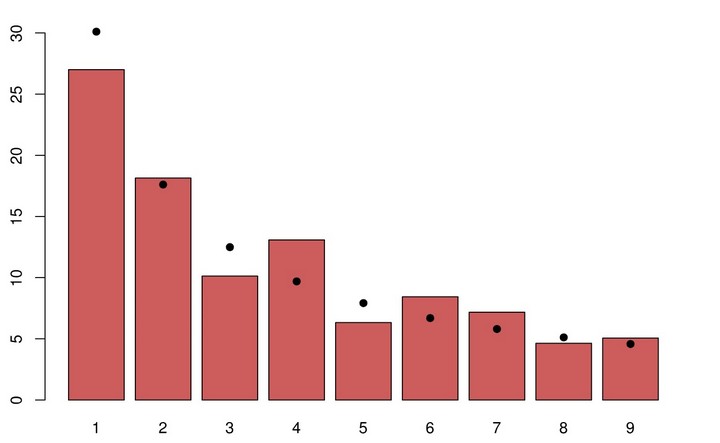
В реальных числовых данных цифра «1» встречается в качестве первой почти в 30% случаев. Цифра «9», наоборот, появляется в начале числа менее чем в 5% случаев. Такие цифры, как «8» и «7», также встречаются реже, чем можно было бы ожидать. Это удивительное распределение обнаруживается в самых разных наборах данных: от численности населения до цен акций и даже длины рек.

Открытие закона

Это явление впервые описал в 1938 году физик Фрэнк Бенфорд. Он заметил, что вероятность появления определённой цифры в начале числа уменьшается по мере увеличения самой цифры. Так, цифра «1» становится первой примерно в 30,1% случаев, «2» — в 17,6%, «3» — в 12,5%, и так далее, вплоть до цифры «9», которая появляется первой лишь в 4,6% случаев.

Простое объяснение на примере билетов

Представим, что у нас есть последовательно пронумерованные лотерейные билеты. Сначала — от 1 до 9: каждая цифра появляется первой с вероятностью 11,1%. Но как только появляется билет номер 10, вероятность того, что число начинается с «1», увеличивается до 18,2%. Когда добавляются билеты с 11 по 19, шанс «1» в начале числа достигает 58%. По мере появления билетов с номерами от 20 и выше, возрастает доля чисел, начинающихся на «2», а вероятность появления «1» постепенно снижается.

Когда закон не работает

Закон Бенфорда не применяется к любым наборам чисел. Например, он не работает с данными, ограниченными узким диапазоном, такими как рост или вес человека. Также закон плохо применим к наборам данных, содержащим всего один или два порядка величин. Тем не менее, во многих других случаях он отлично описывает поведение чисел и часто идёт вразрез с интуитивными представлениями.

Применение закона Бенфорда

Благодаря своей неожиданной, но надёжной предсказуемости, закон Бенфорда активно используется в практике — особенно для выявления мошенничества. Если представленные данные значительно отклоняются от ожидаемого распределения по закону Бенфорда, это может свидетельствовать о том, что числа были подделаны, а не получены в результате объективного измерения.